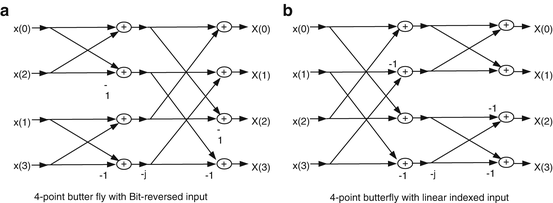
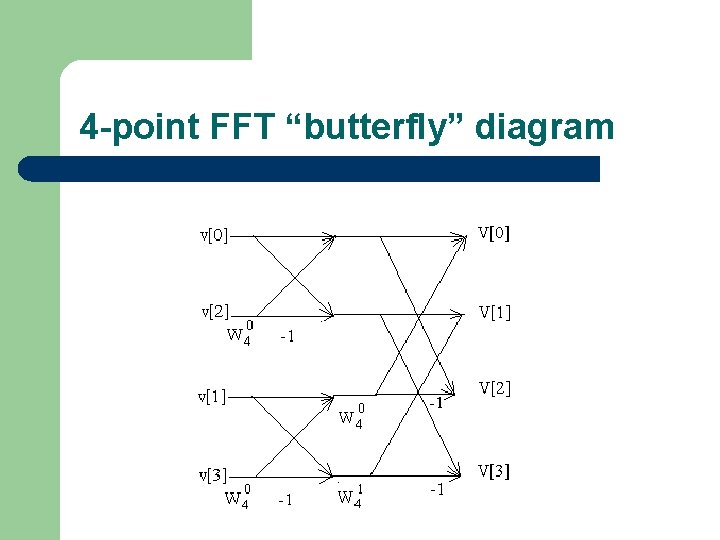
39 4 point fft butterfly diagram

Scribed with vhdl and synthesized on the same state of the art standard cell asic technology than the proposed radix 24 butterfly units. The log is base 2 as described earlier. Signal processing stack exchange is a question and answer site for practitioners of the art and sci...

Implemented the butterfly diagram of 4-point and 8-point DIT (Discrete in Time) Fast Fourier Transform (FFT) using Verilog.

4 point fft butterfly diagram

Abstract-The Fast Fourier Transform (FFT) and Inverse Fast Fourier Transform (IFFT) play vital role in signal processing. It is often used in many communication systems. The proposed paper produces realization of N-bit FFT processor using Radix-4 algorithm. Combined butterfly diagram. 8-point DFT. • In DIT algorithm, we can find that for the output sequence to be in a natural order the input sequence has , find X(k). Decimation In Frequency Fast Frequency Transform. - DIF FFT Definition - Steps of radix 2-DIT FFT Algorithm - 4 point DIF FFT (Flow Graph)... This is how you get the computational savings in the fft. The equations are taken from the textbook on digital signal processing by proakis...

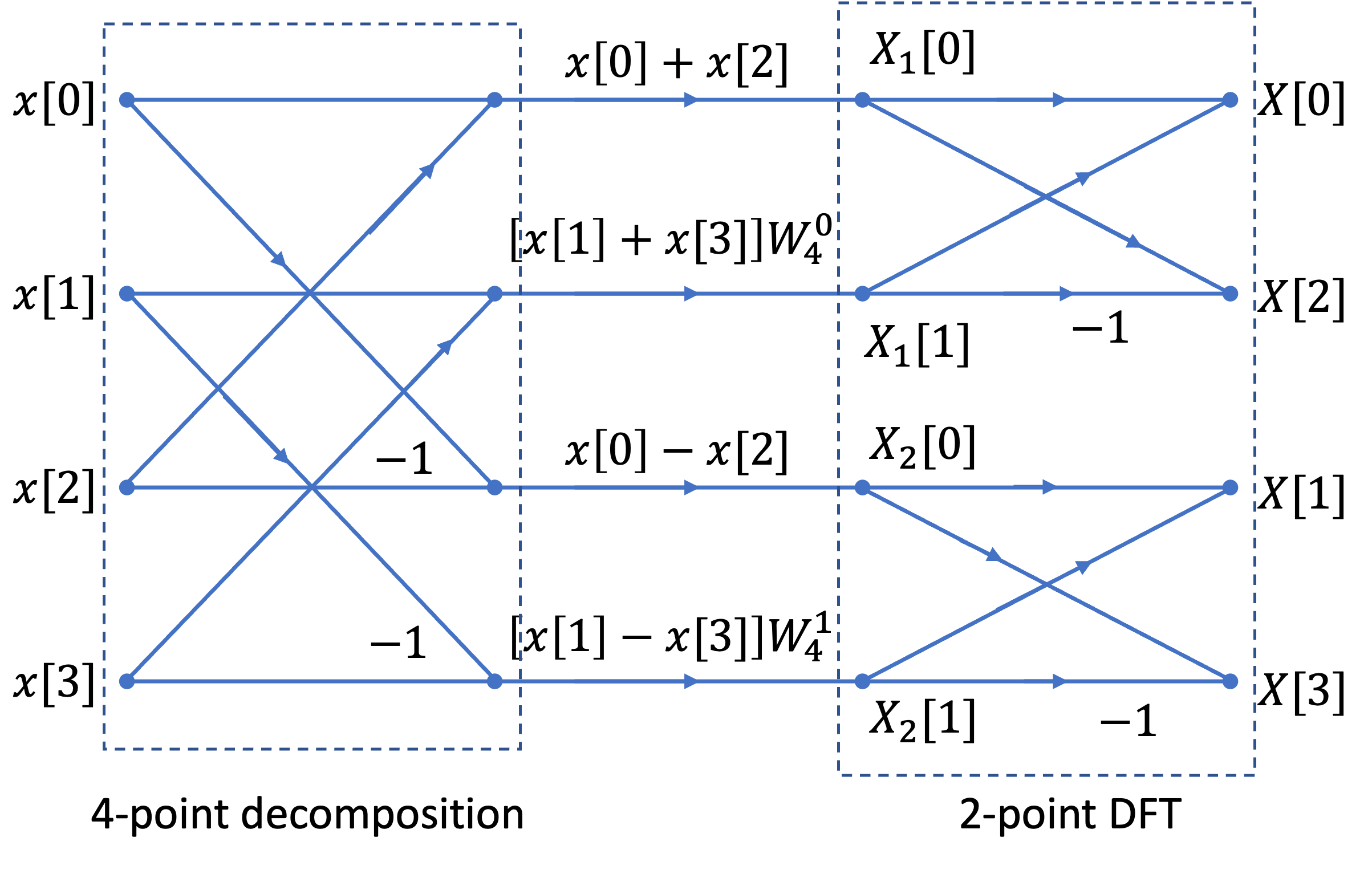
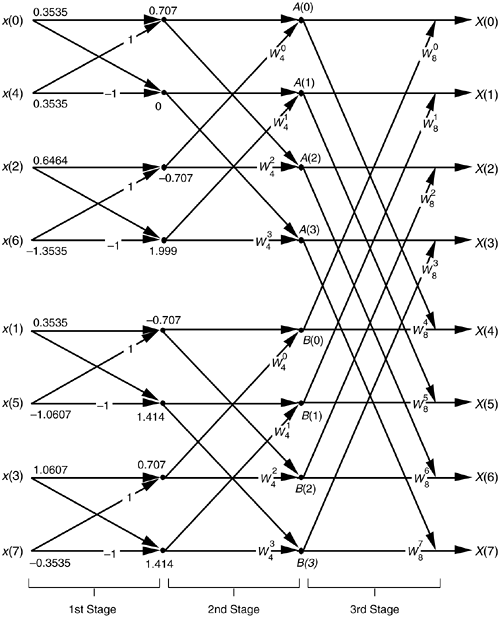
4 point fft butterfly diagram. Radix 2 Fft Signal Flow Tikz Example. The Fourier Transform Part Xii Fft 4. How The Fft Works. Fast Fourier Transform Ppt Download. Comparative Study Of Fpga Implementation Of Parallel 1 D Fft. Pga Implementation Of A Cordic Based Radix 4 Fft Processor. Butterfly Diagram Wikipedia. 4 log4 8. In the context of fast fourier transform algorithms a butterfly is a portion of the computation that combines the results... Download scientific diagram | 4-Point FFT butterfly using Decimation-in-Time. The arrows indicate a weighting by an appropriate twiddle factor, and the complex addition denoted by the '+'. from The basic 4-point FFT [6] is illustrated in Figure 8 for the decimation-in-time implementation. ... This topic is 4 point DIF FFT from the chapter Fast Fourier Transform which has 4 point DIF FFT problems. Building of the Butterfly diagram for a 4 point DFT using the Decimation in time FFT algorithm.

The whole point of the fft is speed in calculating a dft. The radix 4 dif fft divides an n point discrete fourier transform dft into four n... Опубликовано: 2017-05-11 Продолжительность: 12:02 Building of the Butterfly diagram for a 4 point DFT using the Decimation in time FFT algorithm. Reference: The equations are taken from the textbook on Digital Signal Processing by Proakis et al. An FFT is a DFT, but is much faster for calculations. The whole point of the FFT is speed in calculating a DFT. The N Log N savings comes from the fact that there are two multiplies per Butterfly. In the 4 input diagram above, there are 4 butterflies. so, there are a total of 4*2 = 8 multiplies. Block Diagram of a Floating Point. module. To compute the cyclic plane in near real time, the multipliers and adders must be extremely fast. Chapter 3 describes the design of FFTs and cyclic spectrum analyzers in terms of number of FFT butterflies, multipliers and adders.

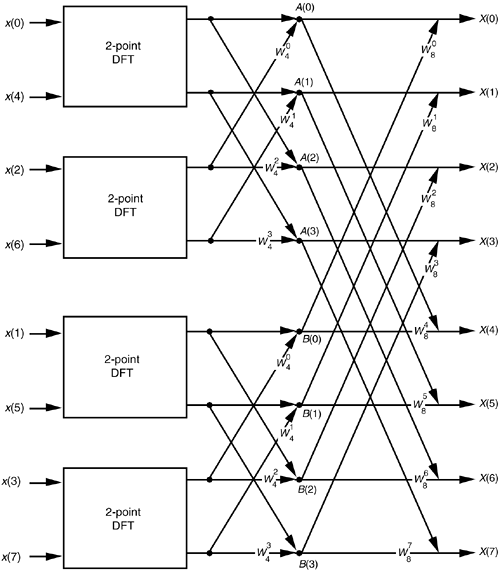
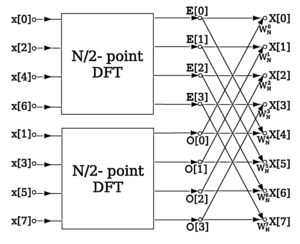
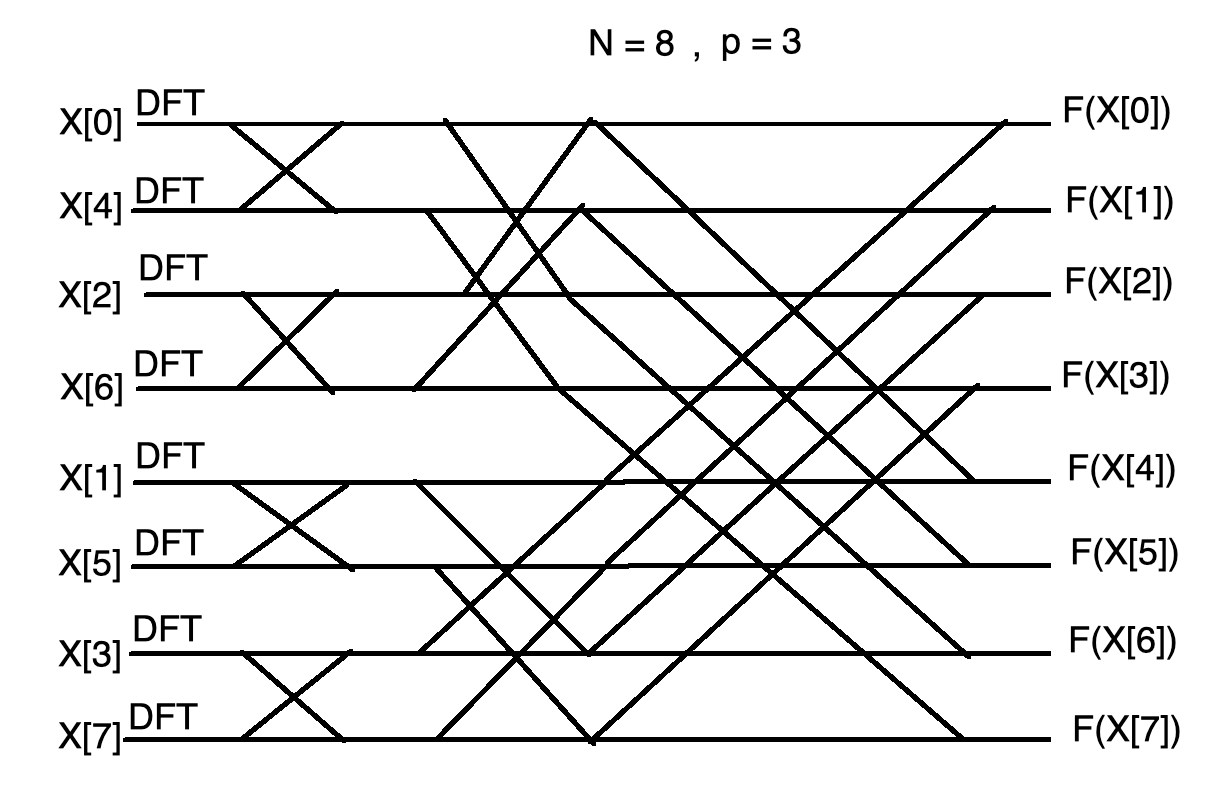
A fast Fourier transform (FFT) is an algorithm that computes the discrete Fourier transform (DFT) of a sequence, or its inverse (IDFT). Fourier analysis converts a signal from its original domain (often time or space) to a representation in the frequency domain and vice versa. The FFT's well-known butterfly pattern of signal flows is certainly evident, and we see the further shuffling of the input data in Figure 4-3. FFT implementation of an 8-point DFT as two 4-point DFTs and four 2-point DFTs. Moving right along, let's go one step further, and then we'll be finished with... FFT is already four times faster than the direct DFT, for N = 21° = 1024. which, not accidentally, is very similar to the two-point DFT diagram pre-sented in Section 12.2 (actually, remembering the second identity of (14.2) we recognize the two-point FFT as a special case of the DIT butterfly). FFT Fast Fourier Transform IFFT Inverse Fast Fourier Transform DFT Discrete Fourier Transformation GPU Graphical Processing Unit CPU Central Processing Unit GPGPU General Processing on GPU CGI Computer Generated Imagery FLOPS oating point operations per second. 4.

Derivation Of The Radix 2 Fft Algorithm Chapter Four The Fast Fourier Transform

Building of the Butterfly diagram for a 4 point DFT using the Decimation in time FFT algorithm. Reference: The equations are taken from the textbook on...

The Fast Fourier Transform (FFT) is an efficient way to compute the Discrete-time Fourier Transform (DFT) by exploiting symmetry and periodicity in FFT butterflies are normally performed sequentially. However, the MRC6011 device has 16 processors that can perform 16 simultaneous butterflies.

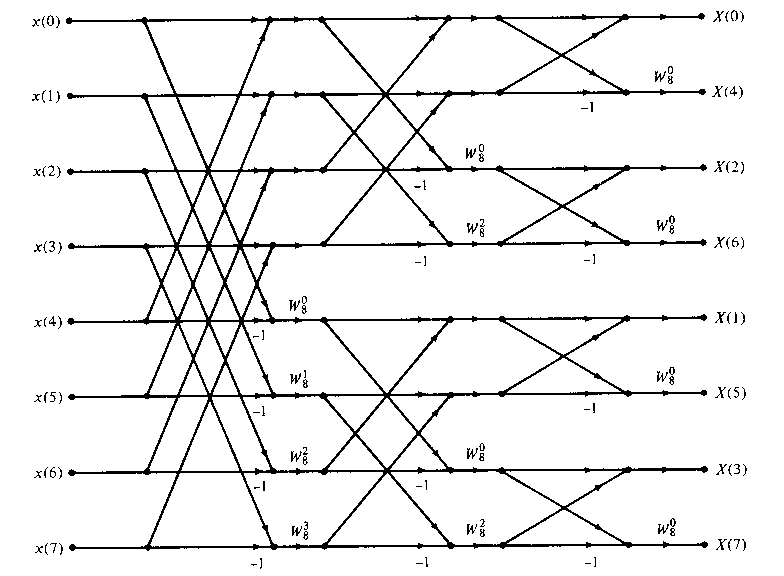
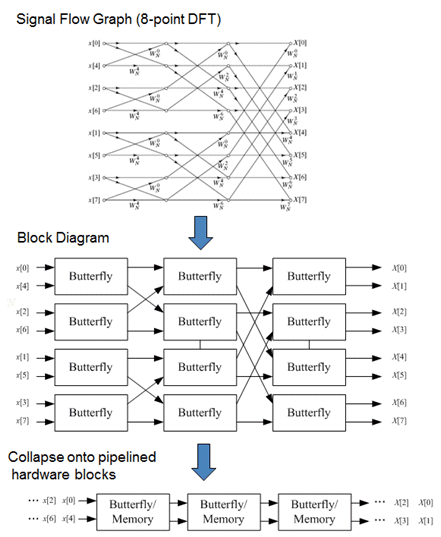
Figure 1. Butterfly diagram for 8-point DFT with one decimation stage. Applying the same decomposition technique again to divide two N/2-points DFTs into four N/4-point Figure 4. Butterfly diagram for 8-point DIF FFT. 4. Implementation. To implement the computation of butterfly with C54x.

Solved A B Draw The Butterfly Diagram Of 4 Point Fft Chegg Com

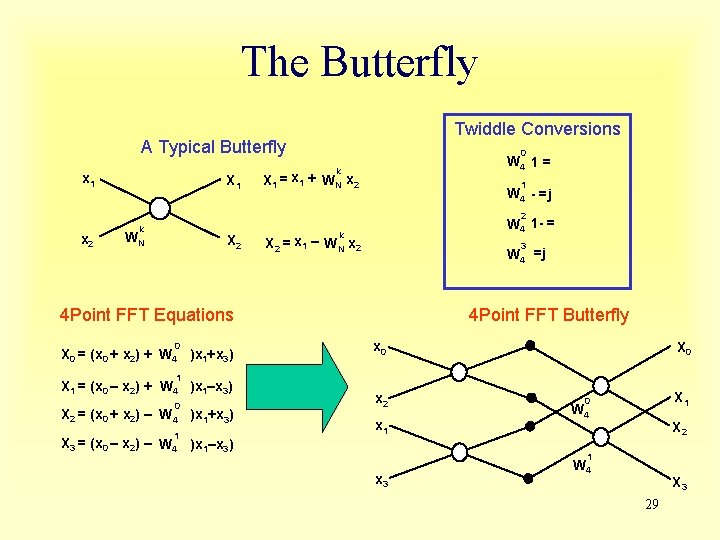
Figure 1. Diagram of Fixed-Point Representations − Integer and Fractional. Floating-point arithmetic consists of representing a number by way of two The basic radix-2 butterfly computation in the DIT FFT algorithm is shown in Figure 4 where both the input and twiddle factors are complex values.

Radix 4 Fft Algorithms Digital Signal Processing A User S Guide Openstax Cnx

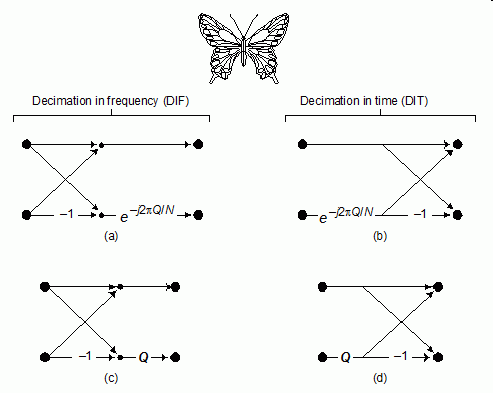
A butterfly diagram is a portion of the computation that combines the results of smaller discrete Fourier transforms (DFTs) into a larger DFT, or vice versa (breaking a larger DFT up into subtransforms). Why the Name 'BUTTERFLY';? 4-POINT FFT BUTTERFLY DIAGRAM.

This article is about butterfly diagrams in FFT algorithms; for the sunspot diagrams of the same name, see Solar cycle. This diagram resembles a butterfly (as in the morpho butterfly shown for comparison), hence the name, although in some countries it is also called the hourglass diagram.

Solved Referencing The 8 Point Fft Butterfly Processing Chegg Com

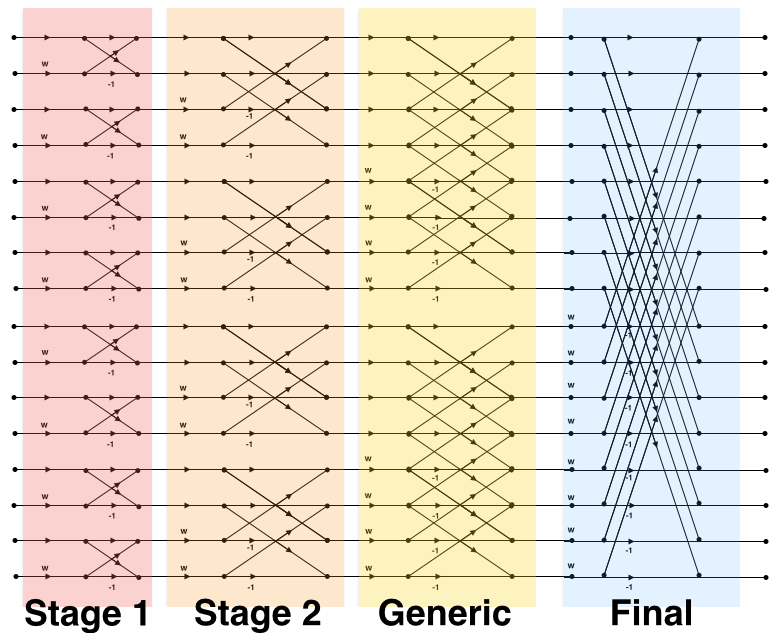
In that diagram of a $16$ point FFT For stage 2: 0 butterflies with 4, 8 butterflies with 12, and so on. Of course stage 2's inputs are stage 1's outputs. My hope is that for each stage of the FFT, I can just have a simple counter going from $0$ to $N-1$ (FFT length $N$), and I can do very inexpensive...

In the context of fast Fourier transform algorithms, a butterfly is a portion of the computation that combines the results of smaller discrete Fourier transforms (DFTs) into a larger DFT, or vice versa (breaking a larger DFT up into subtransforms).

Decimation In Time Dit Radix 2 Fft Digital Signal Processing A User S Guide Openstax Cnx

Radix-2 DIT FFT algorithm Butterfly Diagram- Anna university frequently asked question IT 6502. Building of the Butterfly diagram for a 4 point DFT using the Decimation in time FFT algorithm. Reference: The equations are taken ...

The Fast Fourier Transform Eg 247 Signals And Systems

The equations are taken from the textbook on digital signal processing by proakis et al. First here is the simplest butterflyits the...

Optimizing Fast Fourier Transformation On Arm Mali Gpus Graphics Gaming And Vr Blog Arm Community Blogs Arm Community

Matlab fft butterfly travel. Computes fast fourier transform (FFT) and generates. Details: Figure 3. Butterfly diagram for 8-point DFT with one decimation stage In contrast to Figure 2, Figure 4 shows that DIF FFT has its input data sequence in natural order and the output sequence in bit-reversed order.

The Fourier Transform Part Xiv Fft Algorithm The Mobile Studio

Fast Fourier Transform (FFT). In this section we present several methods for computing the DFT efficiently. In view of the importance of the DFT in various digital signal processing applications, such as linear filtering, correlation analysis, and spectrum analysis, its efficient computation is a topic that has...

Fast Fourier Transform Fft On Gpus Springerlink

This is how you get the computational savings in the fft. The equations are taken from the textbook on digital signal processing by proakis...

Butterfly Diagram Wikipedia

Combined butterfly diagram. 8-point DFT. • In DIT algorithm, we can find that for the output sequence to be in a natural order the input sequence has , find X(k). Decimation In Frequency Fast Frequency Transform. - DIF FFT Definition - Steps of radix 2-DIT FFT Algorithm - 4 point DIF FFT (Flow Graph)...